Memo

0812学习笔记

数据结构

红黑树

RULE

  1. Every node is either black or red.
  2. The root is black
  3. All leaves(NIL/null nodes) are black.
  4. Red node rule : If a node is red ,both its children and parents are black.(no two red in a row)
  5. Black height rule: Every path from a node to its descendant NIL node contains the same number of black nodes.

​

Construction (Insertion)

  1. Case 1: Parent node is BLACK, go ahead.

  2. Case 2: RED parent,See your uncle:

    1. Case 2.1 :BLACK uncle , Rotation to make things in balance.

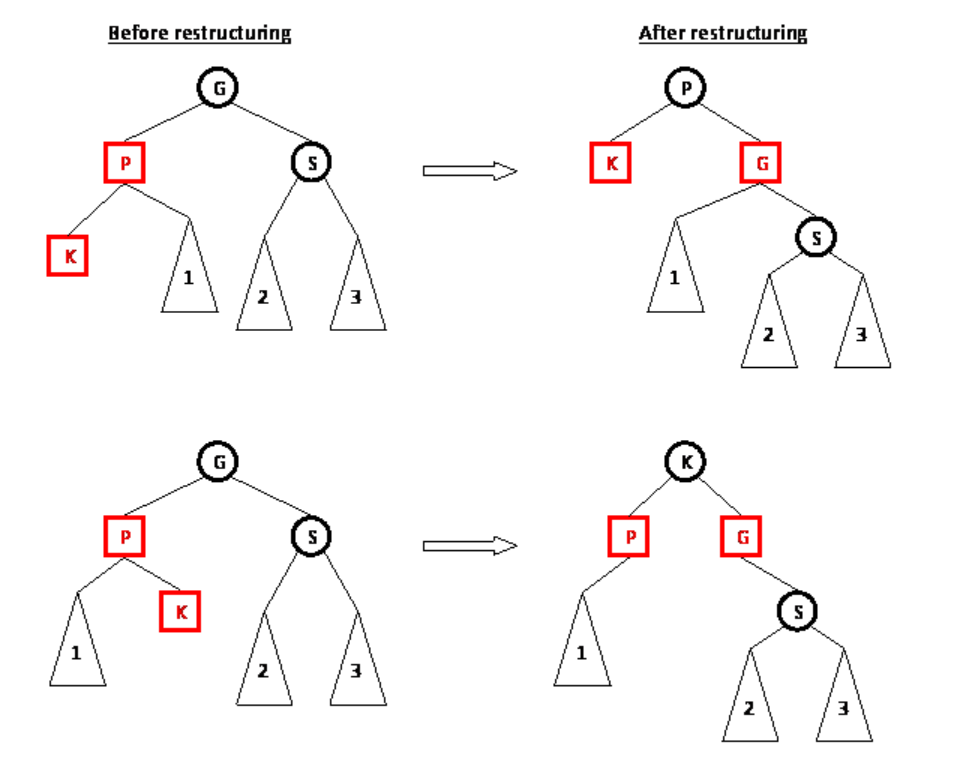
      Case2.1 LL&LR

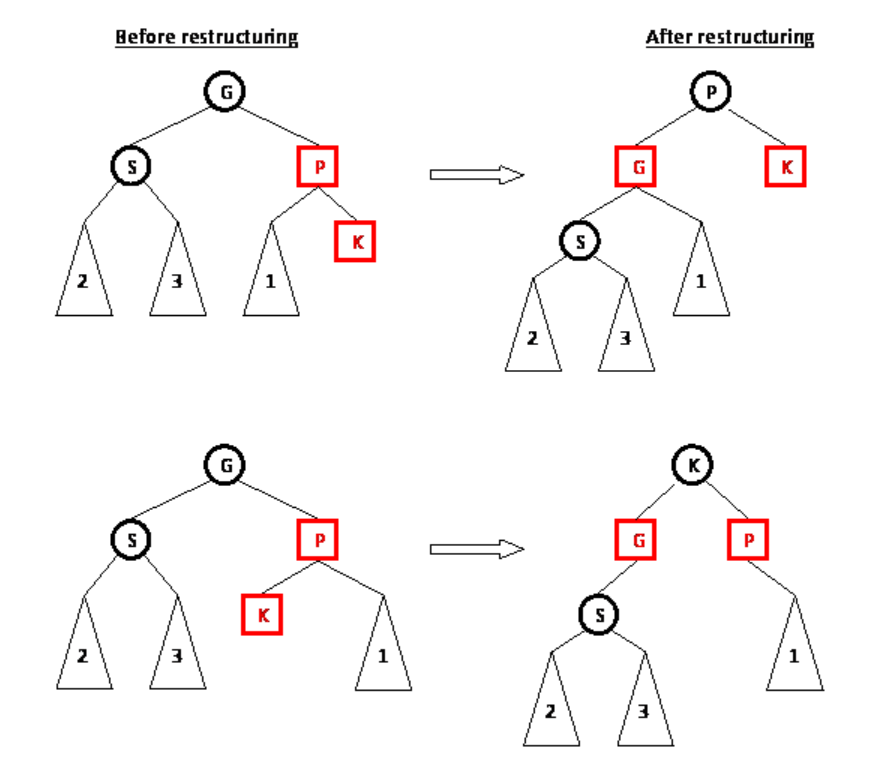
      Case2.1 RL&RR

    2. Case 2.2 :RED uncle, BLACK-lize your parent and uncle,RED-lize your grand.

      Now consider the process of your grand and repeat cases above.

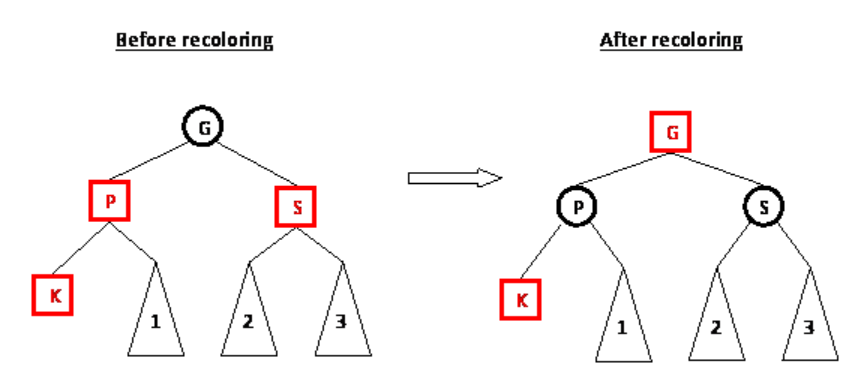
      Case2.2

B树

RULES

Key properties of a B-Tree of order $m$:

  1. Every node can have at most m children
  2. Every node (except root )has at least $\lceil \frac{m}{2}\rceil$ children
  3. Every non-leaf node with $k$ children has exactly $k-1$ keys
  4. Keys in each node are sorted
  5. All leaves appear on the same level
$$ \lfloor\log_{\lceil\frac{m}{2}\rceil}(\frac{n+1}{2})\rfloor +1 \geq h\geq \lceil\log_{m}(n+1)\rceil $$

推理过程

  1. 左式：对于一个m阶的具有n个关键字的B树，其第二层至少有2个结点，第三层至少有$2\lceil\frac{m}{2}\rceil$个结点,以此类推，第$h+1$层至少有$2\lceil\frac{m}{2}\rceil^{h-1}$,这一层为查找失败的叶节点，结点数为$n+1$，因此有
$$ n+1\geq 2\lceil\frac{m}{2}\rceil^{h-1} $$

​ 化简得左式

  1. 右式：对于一个m阶的具有n个关键字的B树，其满足不等式 $$ n\leq (m-1)(1+m+\cdots+m^{h-1})=m^h-1 $$ 化简得右式

Construction(Insertion)

  1. Find the correct leaf Use the same logic as binary search but in multi-key nodes:

    • Compare the new key to the existing keys in the current node.
    • Descend into the correct child pointer until you reach a leaf.

  2. Insert key in sorted order in that leaf.

  3. If the node has ≤ m − 1 keys after insertion → done.

  4. If the node overflows (has m keys):

    • Split the node into two nodes:
      • Middle key moves up to the parent.
      • Left half of keys go to the left child.
      • Right half of keys go to the right child.
    • If the parent also overflows, split it recursively.

  5. If the root splits:

    • Create a new root containing the middle key.
    • The height of the B-Tree increases by 1.

Deletion

  1. If the key is in a leaf → just remove it.
  2. If the key is in an internal node:
    • Replace it with the predecessor (largest in left subtree) or successor (smallest in right subtree).
    • Then delete that replacement key from the leaf.
  3. If a node falls below ⌈m/2⌉ − 1 keys:
    • Borrow a key from a sibling if possible.
    • Otherwise, merge with a sibling.
  4. If the root becomes empty → its only child becomes the new root.